Llevo algunas entradas hablando de un elaborado estudio físico y matemático, realizado por el profesor Jeremy England (puedes leer el paper desde aquí). Voy a intentar en esta entrada explicar, en lo posible, las matemáticas que existen detrás de todo esto.
Primero, repasemos la teoría:
Según el trabajo de Jeremy, la vida es un fenómeno físico más, que sería tan sólo la manifestación del proceso más eficiente de entre los disponibles, para engullir y disipar la energía externa que entra en un entorno abierto y que se encuentra teromodinámicamente lejos del equilibrio.
En el caso concreto de nuestro planeta, la cosa sería como sigue:
La Tierra hace las veces de un sistema local abierto y lejos del equilibro termodinámico. En este sistema, entra constantemente energía externa (ordenada y útil) en forma de fotones que llegan desde el Sol. La atmósfera y el océano, hacen las veces de fuente termal hacia donde disipar la energía absorbida y utilizada en los procesos físicos que tienen lugar. Y, según las matemáticas de este trabajo, la materia disponible se estructura y evoluciona espontáneamente de modo que cada vez se absorba (de la energía externa) y se disipe (hacia la fuente) cada vez más y más energía. De hecho, el mejor modo de disipar más eficientemente energía, es haciendo copias de ti mismo. En otras palabras: si eres bueno disipando energía, y además eres capaz de copiarte a ti mismo, la física te va a ayudar a dominar el entorno. Y las matemáticas parecen apoyar esta hipótesis en el caso de la molécula de ARN, precursora del ADN y de la evolución de la vida (más detalles en el paper).
Ahora veamos e intentemos comprender el estudio desde el punto de vista matemático:
Empezamos considerando un sistema de N partículas invariables en número, de volumen V, en contacto con una fuente de calor de temperatura inversa β, donde:
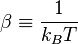
Siendo T la temperatura de la fuente, y kB la contante de Boltzmann. El sistema se encuentra en equilibrio térmico, por lo que la temperatura es espacial y temporalmente uniforme.
En un sistema como este, existen diferentes micorestados i,j, etc, cada uno de los cuales posee su propia energía de estado asociada Ei, Ej, etc
Es decir, que existen sólo cierto número de microestados posibles (estados de las partículas constituyentes del sistema) que permiten mantener constante N, V, y T. Vamos a catalogar dichos microestados permitidos con etiquetas i,j,etc, y a sus energías asociadas con Ei, Ej, etc.
Por otra parte, para sistemas aislados (o casi aislados) como el descrito anteriormente, donde nos encontramos en equilibrio térmico, y donde N y V permanecen constantes, nos encontramos con la propiedad física (parte de la mecánica estadística) denominada distribución de Boltzmann:
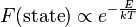
Esta propiedad, nos indica la probabilidad, dado un sistema aislado en equilibrio térmico, de encontrarnos con un determinado microestado (i, j, etc.) de entre los disponibles, teniendo en cuenta únicamente la energía de ese microestado concreto (puesto que T y K son constantes para el sistema).
Y, tras normalizar la distribución de Bolzmann, mediante la partición canónica:

nos queda:

Que nos indica, la probabilidad normalizada de encontrar el micorestado i en un sistema aislado en equilibro térmico, con N, V y T constantes, según sea la energía Ei relacionada con ese microestado.
- Ejemplo 1:
Imaginemos que un átomo tiene sólo dos niveles de energía disponibles, los cuales están separados por 2·10^-23 J (Julios). Si la temperatura del sistema es igual a 1.5 K (grados Kelvin), ¿cuál es la probabilidad de encontrar al electrón en el nivel de más baja energía?
Solución:
Tomamos el nivel de más baja energía Ei = 0 J, y el siguiente nivel Ej = 2·10^-23 J.
La probabilidad de cada estado vendrá dada por:
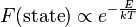
por lo tanto:
F(i) = e^(-0/1.38·10^23·1.5) = 1
F(j) = e^(-2·10^-23/1.38·10^23·1.5) = 0.38
Y, al normalizar el resultado nos da la probabilidad:
p(i) = 72.4% (probabilidad de encontrar el electrón en el estado de baja energía)
p(j) = 27.6% (probabilidad de encontrar el electrón en el estado alta energía)
.
A continuación, y volviendo a la teoría, nos encontramos con la siguiente ecuación[1] que se cumple para sistemas aislados y en equilibrio térmico, como los que estamos estudiando (NVT constante):
Donde observamos la distribución de Boltzmann normalizada que ya hemos visto, y un nuevo elemento multiplicativo: π(i → j; τ )
Este elemento, no es más que la probabilidad condicionada de encontrar el sistema en el microestado j en un tiempo τ (t = τ > 0), sabiendo que al inicio (t = 0) el sistema se encontraba en el microestado i. Y, por otra parte, i* (y j*) son microestados equivalentes a i (y j) pero con momento opuesto (o reverso). Es decir, con un vector momento (y velocidad) igual pero de sentido opuesto.
(1) viene a decir que, en un sistema aislado y en equilibrio térmico (con NVT constantes), la probabilidad de encontrar el micorestado i, multiplicado por la probabilidad condicionada de pasar de i a j en un tiempo τ, es igual, a la probabilidad de encontrar j, multiplicado por la probabilidad condicionada de pasar de j a i en ese mismo periodo de tiempo τ (τ > 0).
Trabajando sobre la ecuación (1), y pasando la probabilidad condicionada π(i → j ; τ ) dividiendo hacia la derecha, y la distribución de Boltzmann normalizada de j dividiendo hacia la izquierda, nos queda la siguiente expresión:
Para llegar a el lado derecho de (2), hemos hecho uso de lo siguiente:

Al dividir una distribución de Boltzmann entre otra, la partición Z se anula, y el exponente se resta, quedando epx {Ei - Ej / kT} = exp { β · (Ei - Ej)}
Sabemos además que el calor transferido a la fuente durante la transición del microestado i al j es:
Qi → j = Ei − Ej, y sabemos que (Qi → j / T) es igual al cambio de entropía que se produce en el baño térmico durante la transición de esos microestados (de i a j), por lo que llegamos a:

y sustituyendo esta expresión, llegamos a (2), a partir de (1), mediante un poco de álgebra.
La ecuación (2) nos indica la relación entre la irreversibilidad de una transición (es decir, cuánto más probable es que ocurra una transición en una dirección i → j que en la dirección reversa u opuesta j* → i*) y el aumento de entropía que se produce en el entorno durante la transición en la dirección i → j.
Hay que hacer notar, además; que aunque todo esto ha sido deducido a partir de sistemas en equilibrio, es igualmente cierto para sistemas lejos del equilibrio.
El resto del trabajo de Jeremy, se enfoca, como veremos, en intentar demostrar que este resultado que acabamos de alcanzar, donde se ha deducido una relación microscópica entre irreversibilidad y entropía, es de aplicación también en un nivel macroscópico y en sistemas lejos del equilibrio termodinámico; como es el caso de las estructuras biológicas autorrreplicativas en la Tierra.
Irreversibilidad macroscópica:
Vamos a intentar determinar las reglas termodinámicas que aplican a nivel macroscópico entre dos estados arbitrarios cualesquiera. Y para lograrlo, tenemos que determinar primero, como se relacionan a nivel microscópico la probabilidad de los microestados con el calor y la entropía.
Con la ecuación (2) ya descubrimos una relación de este tipo para sistemas en equilibrio, pero se ha demostrado[2] que dicha ecuación es generalizable a sistemas microscópicos lejos del equilibrio, siempre y cuando el sistema esté acoplado a un baño (o una fuente) termal, y se componga de microestados reversibles en el tiempo: es decir; que se pueda pasar de i → j y de j → i, en el mismo periodo de tiempo τ (τ > 0), con tan sólo cambiar el sentido del vector momento de las partículas constituyentes.
Si llamamos x(0) al punto inicial en la trayectoria (camino o path) que va desde un microestado cualquiera i, hacia otro microestado en un tiempo τ (τ > 0), y llamamos x(t) al punto final de esta trayectoria, tenemos que se cumple lo siguiente
Esta fórmula, captura una esencial relación microscópica entre calor e irreversibilidad: cuando más probable es una trayectoria frente a su reversa (u opuesta en el tiempo), más aumenta la entropía del Universo mediante la liberación de calor en el baño acoplado al sistema (o, lo que es lo mismo, cuanto más irreversible es una trayectoria seguida, más aumento de entropía produce). Si la probabilidad de la trayectoria hacia delante, es mayor que la probabilidad en sentido opuesto, el camino seguido hacia delante será irreversible, en el sentido de que es muy poco probable que se de el sentido opuesto en dicha trayectoria. Y cuando ocurre esto, el lado izquierdo de la ecuación (la entropía) aumenta.
Además, hay que hacer notar, que toda esta relación entre calor e irreversibilidad, es válida también para sistemas alimentados por fuentes de energía externas siempre que estén sujetas a reversibilidad temporal. Esto quiere decir, que no es necesario que la probabilidad del estado inicial y final de una transición, sigan una distribución Boltzmann, como hemos aplicado hasta ahora.
Si fijamos el punto de inicio y el punto de fin de una trayectoria (por ejemplo, con x(0) = i y x(τ) = j, siendo i y j dos microestados cualesquiera del sistema), y calculamos la media del calor expelido entre los caminos (o paths) disponibles que nos llevan desde i a j (para ir desde un microestado i a otro microestado j, podemos seguir diferentes caminos, y es la media del calor expelido en cada camino posible lo que nos interesa).
Debemos calcular esta media, porque ahora estamos considerando sistemas lejos del equilibrio térmico, y no podemos calcular el calor expelido en el cambio de estado simplemente mediante la diferencia de energía entre los microestado (Qi → j = Ei − Ej) como deducimos a partir de la distribución Boltzmann. Ahora necesitamos calcular el calor expelido en cada camino posible entre los microestados, y usar la media. Si lo hacemos así, y usamos un poco de álgebra en (3) (reescribiendo el logaritmo en (3) como una ecuación exponencial, y sustituyendo x(0) = i y x(τ) = j), llegamos a
Sin duda, esta regla deducida a nivel microscópico (cuando más probable es una trayectoria, frente a la misma trayectoria pero opuesta en el tiempo; más aumenta la entropía del Universo. O, lo que es lo mismo, cuanto más irreversible es la trayectoria seguida por un sistema a nivel microscópico, más aumento de entropía se produce), debe tener consecuencias a su vez a nivel macroscópico. Vamos a investigar y a intentar formalizar las consecuencias a este nivel:
Vamos a comenzar suponiendo un sistema macroscópico, y una condición empírica observable I de dicho sistema. Una condición de ese tipo, podría ser, por ejemplo: "el sistema macroscópico, contiene una bacteria sana (con un potencial replicativo exponencial) en el inicio de su fase de división celular". Si preparamos, a continuación, un sistema, bajo un conjunto de concreto de condiciones de modo que vemos que el critero I es satisfecho, inmediatamente, podemos asociar una distribución de probabilidad p(i|I) que será la probabilidad condicionada implícita de que el sistema esté en un microestado i en particular, dada la condición macroscópica I (que está bajo nuestro control experimental).
En el ejemplo concreto que estamos siguiendo para I, la probabilidad de que el sistema se encuentre en un microestado i, que se corresponda con un microestado donde todas las partículas están distribuidas equitativamente por toda la superficie es muy pequeña, puesto que un microsistema tan homogéneo espacialmente, es poco probable que contenga un macrosistema donde se observe, por ejemplo, una célula sana. Otro macrosistema i, que se corresponda con una distribución de partículas agrupadas en algún punto, es mucho más probable que contenga un macroestado con una célula. Pues es toda esa distribución de probabilidades, la que definimos como p(i|I).
Supongamos, ahora, que dejamos pasar cierto intrervalo de tiempo τ, mientras mantenemos nuestro sistema en contacto con un baño térmico de temperatura inversa β. e introducimos después una nueva condición macroscópica observable II. Nos valdría, por ejemplo, la siguiente: "el sistema contiene dos bacterias sanas (con un potencial replicativo exponencial) en el inicio de sus fases de división celular".
En el momento en que veamos esta nueva condición II ocurrir (tras esperar τ segundos después de la ocurrencia de I), podemos inmediatamente definir la siguiente distribución de probabilidad p(j |II), la cual indicará la probabilidad condicionada de que el sistema se encuentre en el microestado j, conocido que el sistema fue inicialmente preparado para cumplir el macroestado I, que transcurrió un periodo de tiempo τ, y que finalmente se observó cumplirse el macroestado II.
Y ahora que ya tenemos definida la distribución de probabilidad de nuestros macroestados de interés, vamos a intentar trabajar sobre dicha definición para conseguir una definición de su irreversibilidad macroscópica. Podemos escribir:
La eucación (5), indica la probabilidad de que, después de transcurrir otro periodo de tiempo τ, el sistema vuelva a satisfacer la condición macroscópica I.
En nuestro caso de ejemplo concreto; indicarían la probabilidad de que, tras preparar el sistema hasta observar una célula sana en proceso de división I, y de que transcurra un tiempo τ, se observen dos células sanas II (4). Y la probabilidad de que, tras transcurrir otro periodo de tiempo τ, vuelva a cumplirse I; es decir, que en el sistema sólo haya una célula sana de nuevo.
En lenguaje natural, (4) indica el producto del número de microestados que permite la condición II por el número de microestados que permiten I, multiplicado a su vez por la probabilidad de que el microestado i se de, conocido el macroestado condicionante I, multiplicado por último, por la probabilidad de que el microsistema i se traslade a un microsistema j dado en un tiempo τ. O, en otras palabras: la probabilidad de pasar del macroestado I al II, es igual a la suma de productos de cada microestado i permitido por la probabilidad de que ese microestado i se convierta en alguno de los microestados j que permite II.
- Ejemplo 2:
Imaginemos un tablero de 3 en raya, con 3 x 3 = 9 casillas disponibles (el equivalente a un volumen V constante de 3x3x1). En el tablero siempre hay 3, y sólo 3 fichas (número de partículas N constante), el movimiento o cambio de estado se produce de un modo no dirigido, mediante fluctuaciones.
Definimos ahora un macroestado I = "El sistema contiene las 3 fichas en raya", y otro II = "El sistema no contiene las 3 fichas en raya".
Hay 8 modos de colocar las 3 fichas en raya, y como el cambio es fluctuante y aleatorio, la probabilidad de cada uno de estos modos es equivalente. Es decir; que p(i|I) = 1 / 8 = 0.125. Cada tipo de 3 en raya (microestados i, i', etc.), es igual de probable porque no hay discriminación entre ellas (el movimiento es aleatorio y no dirigido).
Hay 729 modos de colocar las 3 fichas en el tablero 3x3, y de ellas, 8 están en tres en raya, luego hay 721 microestados cuyas fichas no están en tres en raya. Cada uno de esos 721 microestados son también igual de probables, por lo que la probabilidad condicionada p(j |II) = 1 / 721 = 0.0014
Por otra parte, pasar de un microestado i (en 3 en raya) a uno j (no en 3 en raya) tiene la probabilidad:
π(i → j; τ ) = 721 / 729 = 0.99 = 99%
Pasar de un microestado j (no en 3 en raya) a uno i (en 3 en raya) tiene la probabilidad:
π(j → i; τ ) = 8 / 729 = 0.01 = 1%
Como este ejemplo además, es discreto (y no continuo), las integrales en (4) y (5) se vuelven sumatorios, por lo que tenemos:
π(I → II) = 721 · [(0.125·0.99) + (0.125·0.99) + (0.125·0.99) + ... + (0.125·0.99)] = 713.79 / 721 (normalizamos) = 0.99 = 99%
π(II → I) = 8 · [(0.0014·0.01) + (0.0014·0.01) + ... + (0.0014·0.01) + (0.0014·0.01)] = 0.08 / 8 (normalizamos) = 0.01 = 1%
Pasar de un macroestado de tipo I a uno tipo II es mucho más probable que pasar de uno tipo II a tipo I, por lo que el proceso es irreversible, en el sentido de que es muy poco probable que, al preparar el sistema de modo que comencemos con un tablero con 3 en raya, al dejarlo después fluctuar, volvamos a encontrarnos en un microestado i de nuevo tras pasar un tiempo τ.
Volvamos a la teoría:
Si ahora realizamos el cociente de π(II → I) sobre π(I → II) [(5) sobre (4)], y si usamos esta expresión,
para despejar π(i → j; τ ), y también usamos la siguiente propiedad: e^ln(x) = x, procedemos del siguiente modo:
Si usamos la definición de entropía de Shannon

para definir la entropía interna de nuestro sistema, podemos escribir

que simboliza el cambio de entropía interna en nuestro sistema de estudio, durante el cambio hacia delante desde el macrosistema que cumple I hacia el macrosistema cumpliendo II. Si a continuación usamos la propiedad que nos dice que, para todo x, e^x ≥ 1 + x, y
que, mediante estas propiedades ya conocidas,
nos llevan inmediatamente a
Sin embargo, de (8) sacamos una conclusión importante: la irreversibilidad macroscópica en la transición de un conjunto de microestados que cumplen I hacia otro subconjunto de microestados que cumplen II, condiciona un estricto límite en la cantidad de entropía que se puede producir en este tipo de transiciones macro.
En resumen:
Cuanto más irreversible es un proceso macroscópico (es decir; cuanto más negativo sea ln[π(II→I)/π(I→II)], o más positivo sea ln[π(I→II)/π(II→I)]), más positiva debe ser la cantidad mínima de entropía producida.
En un próxima entrada, explicaré como Jeremy England hace uso de toda este modelo matemático para defender su propuesta sobre el origen y la evolución de la vida, desde un punto formal y matemático.
Si no puedes esperar, y quieres adelantarte, puedes leer el trabajo completo de Jeremy, en estos dos papers (y en el vídeo de una interesante charla que dio al respecto):
http://arxiv.org/pdf/1412.1875v1.pdf
http://www.englandlab.com/uploads/7/8/0/3/7803054/2013jcpsrep.pdf
https://www.youtube.com/watch?v=e91D5UAz-f4#t=1720
Espero, de todas formas, poder terminar pronto mi análisis personal del resto del trabajo, y publicarlo por aquí.
Un saludo.
[1] C. W. Gardiner, Handbook of Stochastic Methods, 3rd ed. (Springer, 2003).
[2] G. E. Crooks, Phys. Rev. E 60, 2721 (1999).
[3] R. A. Blythe, Phys. Rev. Lett. 100, 010601 (2008).
[4] A. Gomez-Marin, J. M. Parrondo, and C. Van den Broeck, Phys. Rev. E 78,
011107 (2008).
[5] G. Verley, R. Chétrite, and D. Lacoste, Phys. Rev. Lett














No hay comentarios:
Publicar un comentario